La merveilleuse force centrifuge de la Terre
Dès qu'un objet est un rotation,
il est soumis à une force
mystérieuse qui pousse un objet présent à sa
surface à s'éjecter de
sa surface. Plus la vitesse de rotation est élevée plus la
force est importante.
A quoi est due
cette force ?
Cette question fait toujours l'objet d'intenses débats
entre physiciens chevronés. La réponse peut sembler évidente.
C'est
parce que l'objet tourne
qu'il est soumis à cette force !
Si l'on regarde un patineur ou une patineuse tourner autour de
lui (elle)-même, ses bras ont tendance à s'écarter de son corps.
C'est donc parce qu'il tourne qu'il est soumis à cette force !
Ce n'est pas une réponse à la question mais une constatation.
En réalité, la réponse fut trouvée en 1893 par le physicien
autrichien Ernst Mach.

Ce principe est exprimé pour la première fois par Mach dans
son ouvrage The Science
of Mechanics en 1893, mais a été identifié en tant que
principe et baptisé "Principe
de Mach" par
Albert Einstein en
1918.
Einstein était fasciné par les idées de Mach.
En physique théorique, le principe
de Mach est une conjecture
selon laquelle l'inertie
des objets matériels serait induite par « l'ensemble des autres masses
présentes dans l'univers », par une interaction non spécifiée.
En clair, cela veut dire qu'il
existe une interaction mystérieuse entre tous les atomes de l'univers.
Un atome
distant à des millions d'années-lumière de la Terre agit sur un autre
atome présent sur Terre (voir aussi le principe de
non-localité).
Quelques
équations
Essayons maintenant de rentrer dans le vif du sujet avec
quelques équations.
Soit un objet M de masse m
placé sur la surface de la Terre à une latitude \(\lambda\).
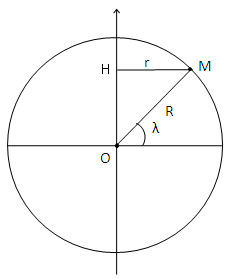
Plaçons-nous dans le référentiel non galiléen terrestre noté R, tournant dans le référentiel géocentrique.
Supposons que le point M est immobile dans ce référentiel.
Dans ce référentiel, l'objet M est soumis à:
- son poids \(\vec{P}=m\vec{g}\).
- la force d'inertie d'entraînement \(\vec{F_{ie}}=m\omega^2\vec{HM}\).
Cette force, axifuge, est la force centrifuge due à la rotation de la Terre.
\(\vec{g}\) est l'accélération de la pesanteur, égale en moyenne à 9.81 m.s-² à la surface de la Terre, et dirigée vers le centre de la Terre.
\(\omega \) est la vitesse angulaire de rotation de la Terre .
Appliquons le principe fondamental de la dynamique (trouvé et formulé par Isaac Newton en 1687) à l'objet M dans le référentiel R.
$$\sum\vec{F}=m\vec{a}$$
Nous avons ainsi:
$$m\vec{a}=m\vec{g} + m\omega^2\vec{HM}$$
Soit à l'équateur, une accélération:
$$\boxed{a=g -R\omega ^2} \space (1)$$
où R est le rayon de la Terre (R=6371 km).
A la calculatrice, nous obtenons une accélération de:
$$a=9.81 - 0.03 = 9.78 \space m.s^{-2}$$
Calculons la vitesse linéaire à l'équateur.
La Terre effectue un tour complet en 24h soir 86400 secondes.
Pendant cette durée elle tourne de 40000 kilomètres.
On en déduit la vitesse:
$$v={d \over T}$$
$$v={40000\cdot 10^3 \over 86400}=463 \space m.s^{-1}$$
Malgré cette vitesse considérable, nous ne sommes pas éjectés de la surface de la Terre car nous sommes fermement attirés par elle par la gravitation universelle.
L'accélération due à la force centrifuge est seulement égale à 0,3% de celle de la gravitation due à la Terre.
Pour que nous soyons éjectés de la surface terrestre, la Terre devrait tourner pendant une durée de période:
$$\boxed {T=2\pi \sqrt {R \over g}}$$
Cette relation est obtenue en annulant l'équation (1).
$$T=5067 \space secondes \space soit \space 1h24m$$
Ce qui donnerait une vitesse linéaire à l'équateur de 7,9 km/s !

